Формирование математической грамотности в начальной школе

Заказ № 2311894

Аннотация. В статье раскрываются способы формирования математической грамотности у младших школьников.

Ключевые слова: математическая грамотность, формы работы.

«Что значит владение математикой? Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности».

Джордж Пойа

Сегодня в мире на первое место выходит потребность очень быстро реагировать на изменения, происходящие в жизни, умение самостоятельно находить, анализировать, применять информацию.

В начальных классах учащиеся начинают применять знания и умения в простейших жизненных ситуациях, если организовать их обучение в соответствии с требованиями к личностным, метапредметным и предметным результатам Федерального государственного образовательного стандарта начального общего образования (ФГОС НОО).

Умение решать текстовые задачи отражено в предметных планируемых результатах ФГОС НОО освоения основной образовательной программы начального общего образования с учетом специфики и содержания предметной области "Математика и информатика".

Функциональная грамотность, это «способность человека решать нестандартные жизненные задачи и различных сферах жизни и деятельности на основе прикладных знаний». Одним из нее видов является математическая грамотность.

«Математическая грамотность – способность человека определять и понимать роль математики в мире, в котором живут, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину».

Функциональная математическая грамотность предполагает способность учащегося использовать математические знания, приобретённые им за время o6yчeния в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе.

Bepнëмся к понятию «математической грамотности» и выделим из него три основных компонента:

1) понимание роли математики в реальном мире;

2) высказывание обоснованных математических суждений;

3) использование математики для удовлетворения потребностей человека.

Для реализации второго компонента необходимо не только развивать математическое мышление обучающихся, но и работать над развитием математической речи, что способствует свободному владению математическими понятиями и способности обучающихся вести грамотный диалог или монолог на уроке, в дискуссии, в жизни. Работа над развитием математической речи подразумевает обучение правильному использованию математических терминов в речи, развитие связной математической речи и формирование культуры математической речи. Для каждого направления работы разработаны соответствующие упражнения.

В рамках почти любой темы можно поставить перед учащимся проблемы вне предметной области, которые решались бы с помощью знаний, полученных при изучении того или иного предмета.

Математика предоставляет хорошие возможности для рассмотрения подобных задач.

На уроках математики чаще, чем на других уроках учащиеся сталкиваются с текстовыми задачами различного содержания и привычным образом составляют модель для применения математических знаний для конкретной задачи.

Поэтому математическая грамотность – одна из составляющих функциональной грамотности.

При формировании функциональной грамотности на уроках математики возникает ряд трудностей.

1. Учащиеся испытывают затруднения, связанные с избирательным чтением. Они не могут выделить существенную информацию, вопрос и данные, важные для решения задачи. В своей работе я сталкивалась с тем, что ученик, видя нестандартную задачу, не приступал к решению, только из-за того, что его пугает большое количество данных или большой объём текстовой информации. Хотя со стандартными задачами из учебника ученик справляется. Невнимательность к прочтению условия, непривычность и необычность формулировок пугает обучающихся. Поэтому математическая компетентность невозможна без читательской компетентности.
2. Проблема при формировании математической функциональной грамотности: как сформулировать (переформулировать) задачу, чтобы найти тот математический аппарат, с помощью которого уже можно решить привычную математическую задачу? Оценить математические связи между событиями. Это и есть основная проблема для школьника.
3. Немаловажная проблема возникает при интерпретации результата, полученного математическими вычислениями, обратный перевод с математического языка на язык решаемой проблемной задачи. Очень часто учащиеся, получив ответ при решении задачи, не задумываются, возможен ли такой результат в реальности.

И тогда мы можем получить в ответе: отрицательную строну квадрата, отрицательную скорость движения или не целое число строителей и т.п.

Данные проблемы могут решаться только в комплексном подходе к формированию функциональной, в частности, математической компетентности.

Вывод: учащиеся, овладевшие математической грамотностью, способны:

• распознавать проблемы, возникающие в окружающей действительности, которые могут быть решены средствами математики;
• формировать проблемы на языке математики;
• решать проблемы, используя математические знания и методы математического моделирования;
• интерпретировать полученные знания;
• формулировать и записывать окончательные решения.

В ходе уроков математики развивается математическая культура учащихся в целом. В понятие математическая культура входят: алгоритмическая культура, вычислительная культура, графическая культура, логическая культура, математическая грамотность. Дополнительные задания, применяемые в системе на различных этапах урока, позволяют развивать различные компоненты математической грамотности.

Таким образом, цель учителя научить учащихся добывать знания, умения, навыки и применять их в практических ситуациях, оценивая факты, явления, события и на основе полученных знаний принимать решения, действовать.

Задачи на формирование математической грамотности, изучаемые в 4 классе.

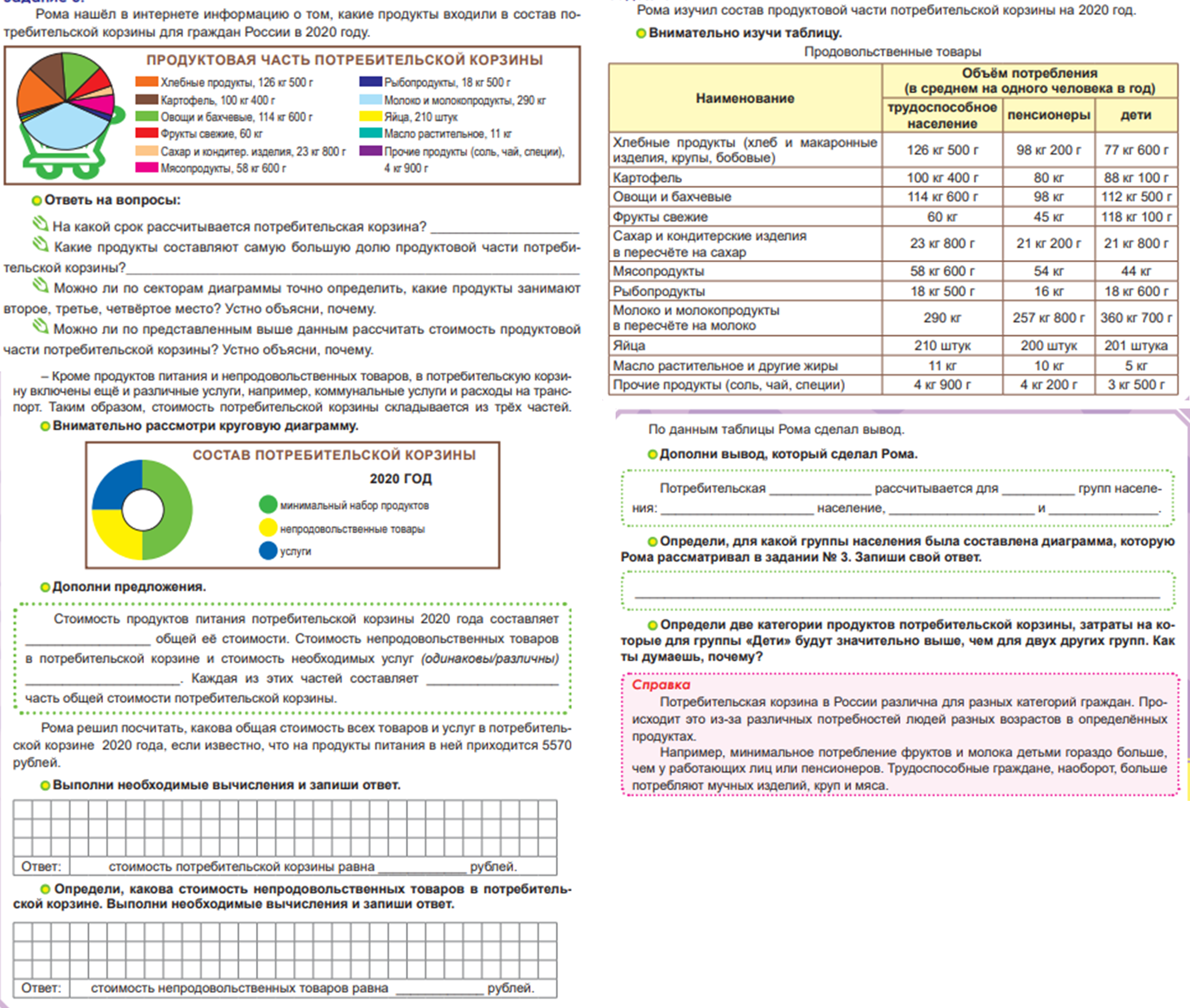
Виды работ, используемых на уроках математики, способствующие развитию функциональной математической грамотности младших школьников.

1. Работа над задачей.

Многие ученики только после повторного анализа осознают план решения задачи. Это путь к выработке твердых знаний по математике.

2. Решение задач разными способами.

Мало уделяется внимания решению задач разными способами в основном из-за недостатка времени. Но это умение свидетельствует о достаточно высоком математическом развитии.

3. Представление ситуации, описанной в задаче и её моделирование:

а) с помощью отрезков.

Мышка встречала гостей. Лиса пришла раньше Медведя, Волк позже Зайца, Медведь раньше Зайца, Сорока позже Волка.

Кто пришёл раньше всех? Кто пришёл позже всех? В каком порядке приходили гости? (обозначь на отрезке)

б) с помощью рисунка.

На грядке сидели 6 мышек. К ним подбежали ещё 3. Кот подкрался и схватил одну. Сколько мышек осталось на грядке?

в) с помощью чертежа.

Обращаю внимание детей на детали, которые нужно обязательно представить, и которые можно опустить.

4. Разбивка текста задачи на значимые части.

5. Решение задач с недостающими или лишними данными.

Работа над задачей с недостающими и лишними данными воспитывает у детей привычку лучше осмысливать связи между искомым и данными.

Задача: В первом букете ромашки. Это на 12 ромашек больше, чем во втором букете. Сколько ромашек в двух букетах?

6. Самостоятельное составление задач учениками.

1) используя слова: больше на несколько, меньше на несколько единиц, в несколько раз больше, в несколько раз меньше;

2) по данному плану ее решения,

3) действиям и ответу;

4) по выражению и т. д.

7. Объяснение готового решения задачи.

8. Изменение вопроса задачи.

У Иры 5 роз, а у Оли на 2 розы меньше. Сколько роз у Оли?

Измени вопрос так, чтобы задача решалась в 2 действия.

9. Составление разных выражений к данным задачам

10. Выбор выражений, которые являются решением задачи.

11. Выбор способа записи решения задачи (выражением, уравнением, по действиям, с пояснением, с вопросами)

12. Использование приема сравнения задач и их решений.

13. Выбор решения из двух предложенных (верного и неверного).

14. Изменение условия задачи так, чтобы задача решалась другим действием.

15. Закончить решение задачи.

16. Составление аналогичной задачи с измененными данными.

17. Составление и решение обратных задач.

Литература:

1. Дюкарева О.А. Развитие математической грамотности младших школьников / Школьная педагогика. 2021. №1. С.7-8.
2. Авдейчик Е.А. Формирование функциональной (математической) грамотности на уроках математики в начальных класса средствами ОС Л.В. Занкова // Социальная сеть работников образования nsportal.ru. 2014. 24 дек. URL: http://nsportal.ru/nachalnaya-shkola/raznoe/2014/12/24/formirovanie-funktsionalnoy-matematicheskoy-gramotnosti-na
3. Архипова Т.В. Формирование математической культуры в обучении младших школьников // Социальная сеть работников образования nsportal.ru. 2014. 25 сен. URL: http://nsportal.ru/nachalnaya-shkola/dlya-kompleksov-detskii-sad-nachalnaya-shkola/2014/05/21/diplom-formirovanie
4. Базарнова Е.Н. Формы работы на уроках математики в процессе решения текстовых задач // Сайт «Фестиваль педагогических идей «Открытый урок». 2014. 4 сен. URL: http://referatwork.ru/refs/pedagogics/ref-6148.html