Решение олимпиадных задач на взвешивание монет

Заказ № 2088798

Данная работа является результатом нашей исследовательской деятельности, осуществляемой в школьном математическом кружке, который действует на базе МАОУ СОШ №7 г. Туймазы. На выполнение этого комплекса исследований, начиная от выдвижения гипотез, заканчивая получением и обработкой результатов, ушло 2 года. Данная тема нашего исследования возникла неслучайно. Дело в том, что задачи на взвешивание монет, в результате которых необходимо определить за минимальное количество взвешиваний фальшивую монету, очень часто встречаются на олимпиадах разного уровня, для школьников нашего возраста, но нигде мы не встречали систематизированных методических пособий, изучая которые можно было бы научиться успешно решать задачи данного типа. В разных пособиях встречаются лишь единичные задачи с их решением. Исходя из вышеизложенного, я попытался ликвидировать этот пробел, вставляя закономерность между количеством взвешиваемых монет, и минимальным количеством взвешиваний, необходимыми для определения фальшивой монеты. Кроме этого, передо нами были поставлены и более конкретные задачи: решить эту задачу для ста различных случаев (меньшее количество случаев считаю не корректным для выявления закономерности); обработка полученных результатов в виде уравнений и в виде графиков.

Актуальность исследования

Задачи на взвешивание монет, в результате которых необходимо определить за минимальное количество взвешиваний фальшивую монету, очень часто встречаются на олимпиадах разного уровня, для школьников нашего возраста, но нигде мы не встречали систематизированных методических пособий, изучая которые можно было бы научиться успешно решать задачи данного типа (ФМ)

Цель работы – найти и описать алгоритмы решения таких задач. Задачи на взвешивание относятся к типу задач комбинаторного поиска; их решение сводится к работе с информацией.

Задачи:

1) выявить спорные вопросы математики.

2) изучить историю появления монет.

Объект исследования – взвешивания монет

Предмет исследования приемы решение олимпиадных задач на взвешивания.

Теоретическая значимость исследования заключается в систематизации материала по данной теме

Практическая значимость: полученные знания могу быть использованы на уроках математики, на семинарных занятиях, проведение мастер-класса с учащимися 5-6 классов.

Методы исследования - изучение литературы и поиск и анализ информации по данной теме, а также анализ полученных данных.

Глава II. Решение олимпиадных задач на взвешивания

Задачи на взвешивание - достаточно распространённый вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между соб

II.1. Алгоритм взвешивания

3.1. Формулировка задачи.

Какое минимальное количество взвешиваний нужно произвести на чашечных весах, чтобы определить фальшивую (лёгкую) монету, если известно, что количество монет равно n.

3.2. Решения нескольких примеров для демонстрации (3).

При условии, что количество монет будет равным 16, тогда нужно поделить данное число на три группы, таким образом: I=5; II=5; III=6. Произведем взвешивание первой и второй группы между собой, если они окажутся равны, то делим третью группу на три группы: IV=2; V=2; VI=2. Произведем взвешивание четвертой и пятой группы между собой, если они равны, то делим шестую группу на две группы по одной монете каждая и взвешиваем их между собой, если четвертая или пятая группа оказалась легче, проводим аналогичные действия с более легкой группой. Если первая или вторая группа при взвешивании оказалась легче, тогда делим ее на три группы VII=2; VIII=2; IX=1. Взвешиваем между собой седьмую и восьмую группу, если они равны, то монета из девятой группы фальшивая. Если седьмая или восьмая группа легче, то производим деление монет на две группы по одной монете каждая и взвешиваем их каждая между собой. Значит количество взвешиваний в этом случае равно 3.

При условии, что количество монет будет равным 32, тогда нужно поделить данное число на три группы, таким образом: I=11; II=11; III=10. Произведем взвешивание первой и второй группы между собой, если они окажутся равны, то делим третью группу на три группы: IV=3; V=3; VI=4. Взвесим между собой четвертую и пятую группу, если они окажутся равны, то делим шестую группу на три группы: VII=1; VIII=1; IX=2. Взвесим между собой седьмую и восьмую группу, если одна из них легче, та монета и фальшивая, если они равны, то девятую группу делим на две группы по одной монете каждая, взвешиваем их между собой, и та, что легче фальшивая. Если при взвешивании седьмой и восьмой группы, они оказались равны, то делим девятую группу на две группы по одной монете, взвешиваем их, и та, что легче фальшивая. Если при взвешивании первой и второй группы одна оказалась легче, то делим эту группу на три группы: X=4; XI=4; XII=3. Взвешиваем между собой десятую и одиннадцатую группу, если они равны, то делим двенадцатую группу на три группы по одной монете, взвешиваем между собой две из них, и та, что легче фальшивая, а если они равны, то фальшивая та, что отложили. Значит количество взвешиваний для данного случая равно 4.

При условии, что количество монет будет равным 83, тогда нужно поделить данное число на три группы, таким образом: I=28; II=28; III=27. Взвешиваем между собой первую и вторую группу, если они равны, то берем третью группу и делим её на три группы по девять монет (IV;V;VI), взвешиваем между собой четвертую и пятую группу, если они равны, то делим шестую группу на три группы по три монеты (VII;VIII;IX), взвешиваем между собой седьмую и восьмую группу, если они равны, то берем девятую группу делим ее на три группы по одной монете каждая, взвешиваем между собой две из них, и если одна из них легче, то она фальшивая, если они равны, то фальшивая та, что отложили. Если при взвешивании седьмой и восьмой группы, одна из них оказалась легче то проводим те же действия, что и с девятой группой. Если при взвешивании четвертой и пятой группы оказалось, что одна из них легче, то производим те же действия, что и с шестой. Если при взвешивании первой и второй группы оказалось, что одна из них легче, то делим эту группы на три группы таким образом: X=9; XI=9; XII=10. Если при взвешивании десятой и одиннадцатой группы оказалось, что одна из них легче то производим с этой группой те же действия, что и с шестой группой. Если при взвешивании десятой и одиннадцатой группы оказалось, что они равны, то делим эту группу на три группы: XIII=3; XIV=3; XV=4. Взвешиваем между собой тринадцатую и четырнадцатую группу, если одна из них оказалась легче, то производим с этой группой те же действия, что и с девятой группой, Если же они равны, то делим пятнадцатую группу на три группы: XVI=1; XVII=1; XVIII=2. Взвешиваем между собой шестнадцатую и семнадцатую группу, та, что окажется легче фальшивая, если они оказались равны, то делим восемнадцатую группу на две группы по одной монете, взвешиваем их между собой, та, что легче фальшивая. Значит количество взвешиваний в данной задаче равно 5.

3.3. Таблица зависимости количества монет от количества взвешиваний.

На основе исследований для наглядности при дальнейшем изучении была построена таблица зависимости количества монет от количества взвешиваний. Диапазон таблицы от 1 до 100 монет. X здесь количество монет, а Y количество взвешиваний.

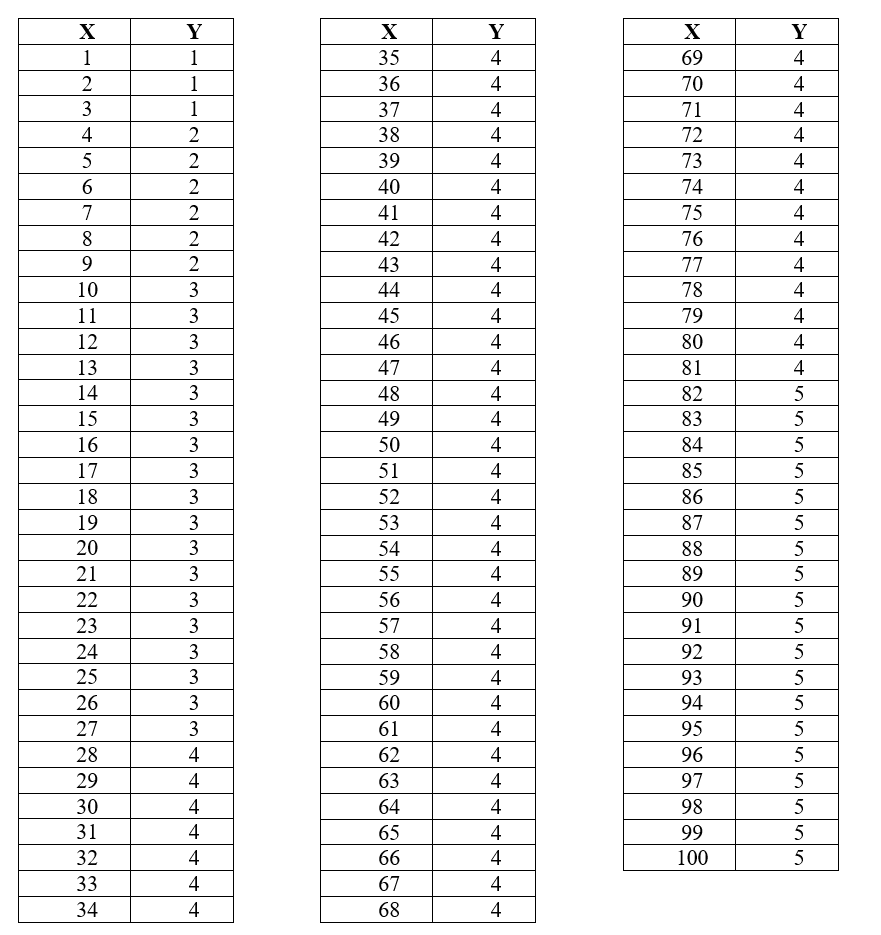
3.4. Таблица уравнения зависимости количества взвешиваний от количества монет.

В результате последующих исследований нам все-таки удалось вывести формулу нахождения числа взвешиваний для числа монет. В данной таблице X это пересечения количества монет, у которых разное количества взвешиваний. K это коэфицент. Формула, предоставленная в данной таблице, имеет вид Y=X-K, где Y количество взвешиваний, и эта формула нужна для нахождения следующего пересечения, а значит, зная пересечения можно без решения сказать, сколько взвешиваний нужно для определения фальшивой монеты.

В данной таблице везде кроме первого случая мы умножаем на 3 и прибавляем K, а умножаем мы предыдущее K, также мы видим, что каждый раз прибавляемое число увеличивается на 2 и является нечетным, а значит имеет чёткую закономерность, и благодаря этому способу можно с лёгкостью найти следующее пересечение.

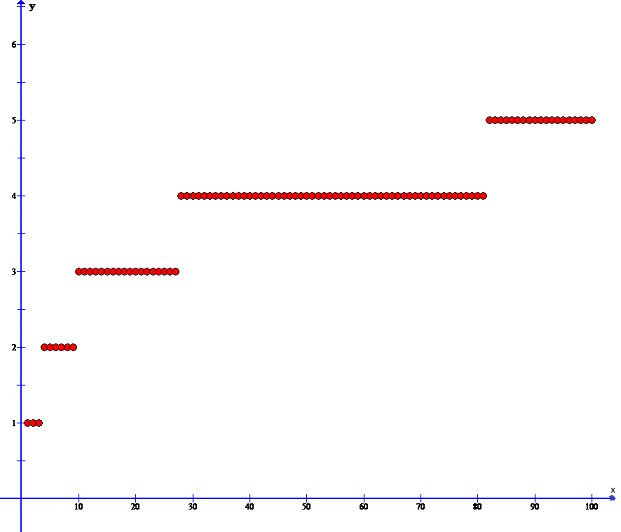
3.5. График зависимости количества взвешиваний от количества монет.

По имеющимся данным, мы построили график зависимости количества взвешиваний от количества монет, где Y количество взвешиваний, а X количество монет.

На этом этапе мы провели опрос среди учащихся нашей школы. Для того что бы выяснить, как часто они решают олимпиадные задачи. Мы задали всего 3 вопроса.

Для проведения опроса мы выбрали 245 учеников. Для удобства восприятия информации мы предложили опрошенным оценить частоту решение олимпиадных задач.

ВОПРОСЫ АНКЕТЫ

1. Желаее ли принять участие в математической олимпиаде?
2. Как часто, вы решаете олимпиадные задачи на взвешивания?
3. Назовите положительные и отрицательные моменты при решение.

Ребятам желающим принять участие были предложены по классам олимпиадные задачи различных типов. Выполнение которых отражено в таблице.

Выводы по главе II

Таким образом нам удалось в течение 2 учебных лет полностью справиться с целями и задачами, поставленными передо нами моим руководителем и смыслом, и содержанием моей творческой деятельности. Действительно я решил сто задач по данной теме, систематизировал и обобил полученные результаты, и оформил их в виде графиков, соответствующих функции, используя выведенную зависимость между количеством монет и минимальным количеством взвешиваний.

4. Заключение.

В ходе нашего исследования мы выявили спорные вопросы математики, которых оказалось очень много, а также изучили историю возникновенния монет.

Работа по данной теме осуществлялась в соответствии с планом исследования, были определены объект, предмет, гипотеза. Были указаны методы исследования, обоснована актуальность. В ходе исследования определили алгоритм решение олипиадных задач Таким образом, нам удалось реализовать все цели и задачи, поставленные перед выполнением этой исследовательской работы

Мы считаем, данная работа имеет перспективы для дальнейшего исследованияСчитаем что практическая значимость данной работы заключается в следующем: изучив литератур по данному вопросу получили дополнительные знания в области метемтики, укрепив свой интерес у этой науке.

Литература:

1. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. М.: Просвещение, 1988.
2. Перельман Я.И. Занимательная геометрия. М.: ГИФМЛ, 1959.